SSGG 7 - Continuous and Discontinuous Modelling of Fracture in Concrete Using FEM
…
417 pages
1 file

Sign up for access to the world's latest research
AI-generated Abstract
This research addresses the modeling of fracture in concrete using Finite Element Method (FEM), analyzing both continuous and discontinuous approaches. The study highlights the necessity of incorporating microstructural characteristics into classical constitutive laws to accurately represent strain localization and size effects. Both monotonic and cyclic loading conditions are simulated, utilizing various continuum models and formulations to capture macro-crack formation and mesh-objective results.
Figures (410)






































































































![Fig. 5.27 Relationship between calculated normalized loads: P(Ex,bt) and PAf,bt) during uniaxial tension (with /=5 mm) and ratio h/], as compared to size effect law by Bazant (2003) within: a) damage mechanics, b) elasto-plasticity (Bobinski and Tejchman 2006)](https://figures.academia-assets.com/37013038/figure_109.jpg)


































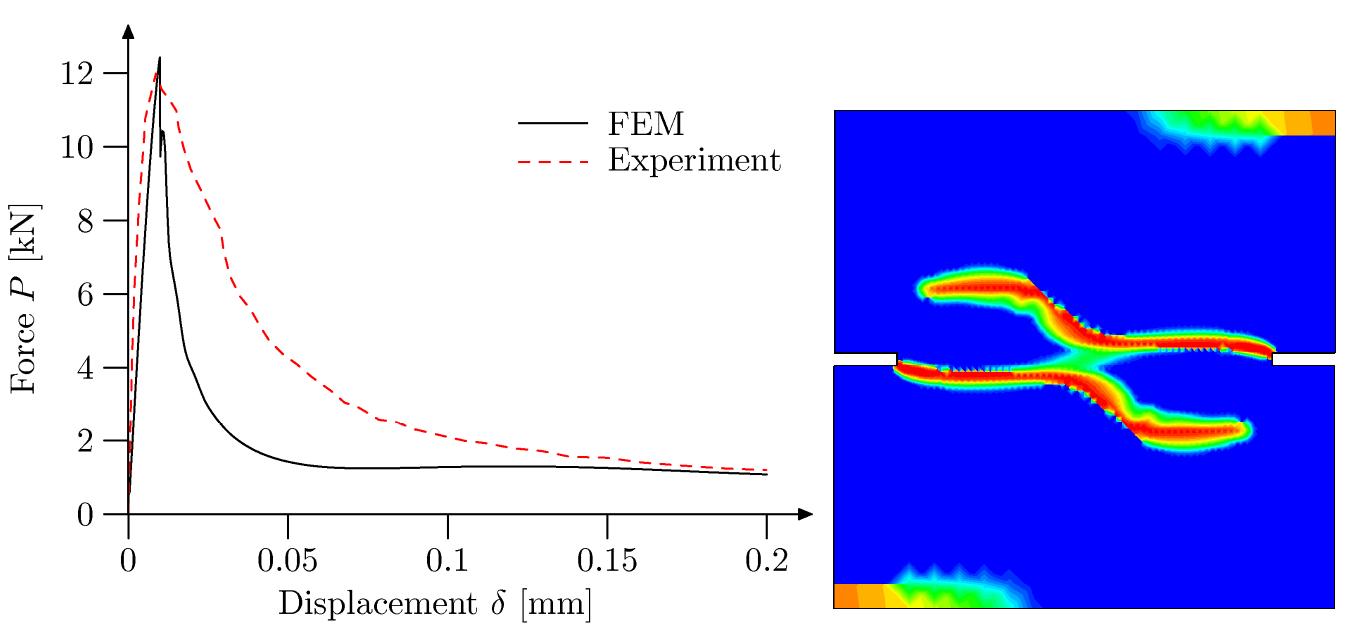

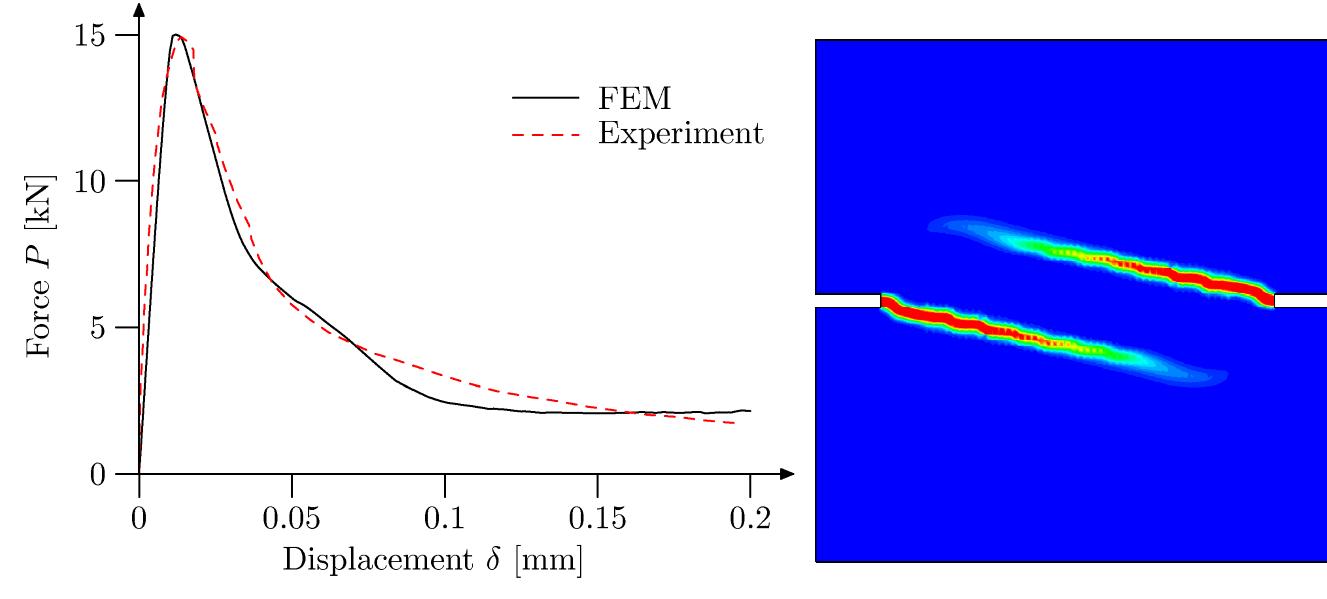






















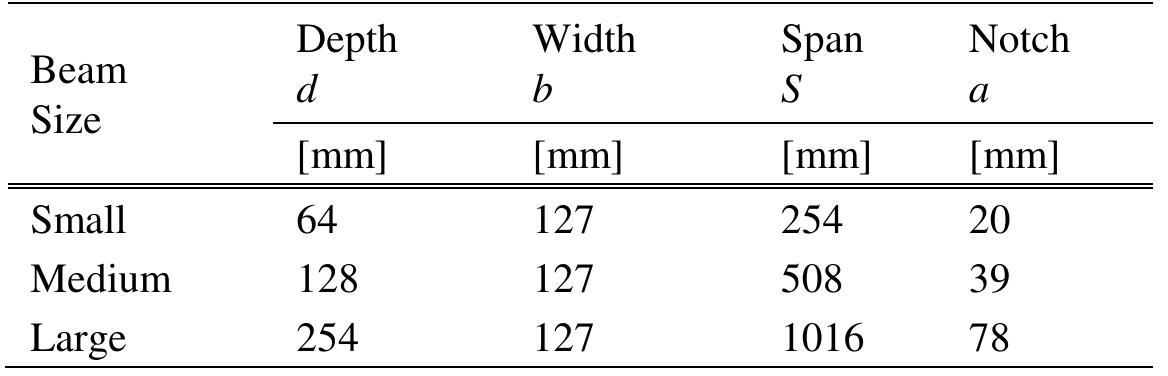
















































































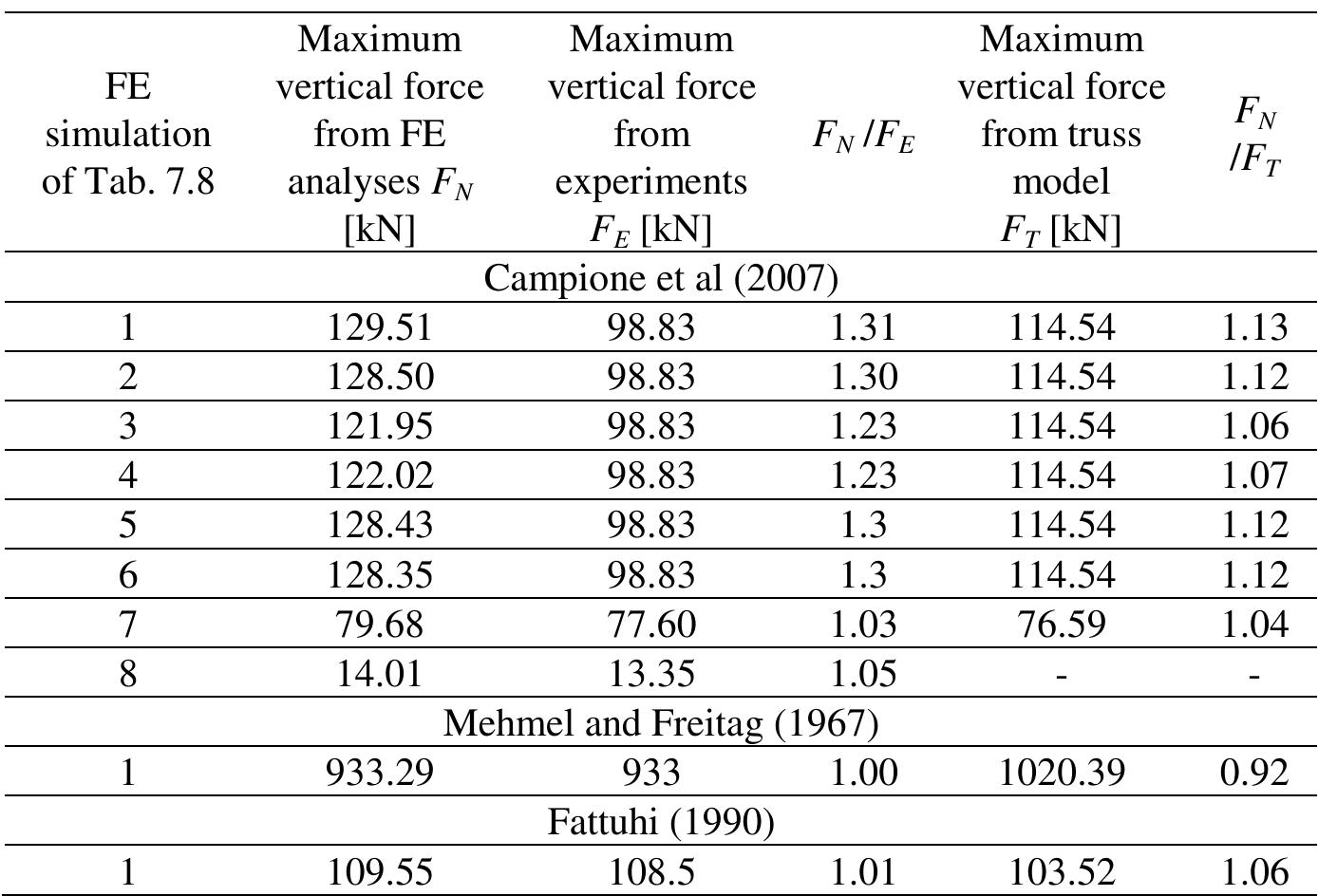
![[1] Kim and Lee (2000), [2] Hsu (1988), [3] Lloyd and Rangan (1996), [4] Bazant and Kwon (1994).](https://figures.academia-assets.com/37013038/table_014.jpg)











































![Fig. 8.7 The correlation distances for different coefficients 2 [1/m] (Bobinski et al. 2009)](https://figures.academia-assets.com/37013038/figure_285.jpg)









































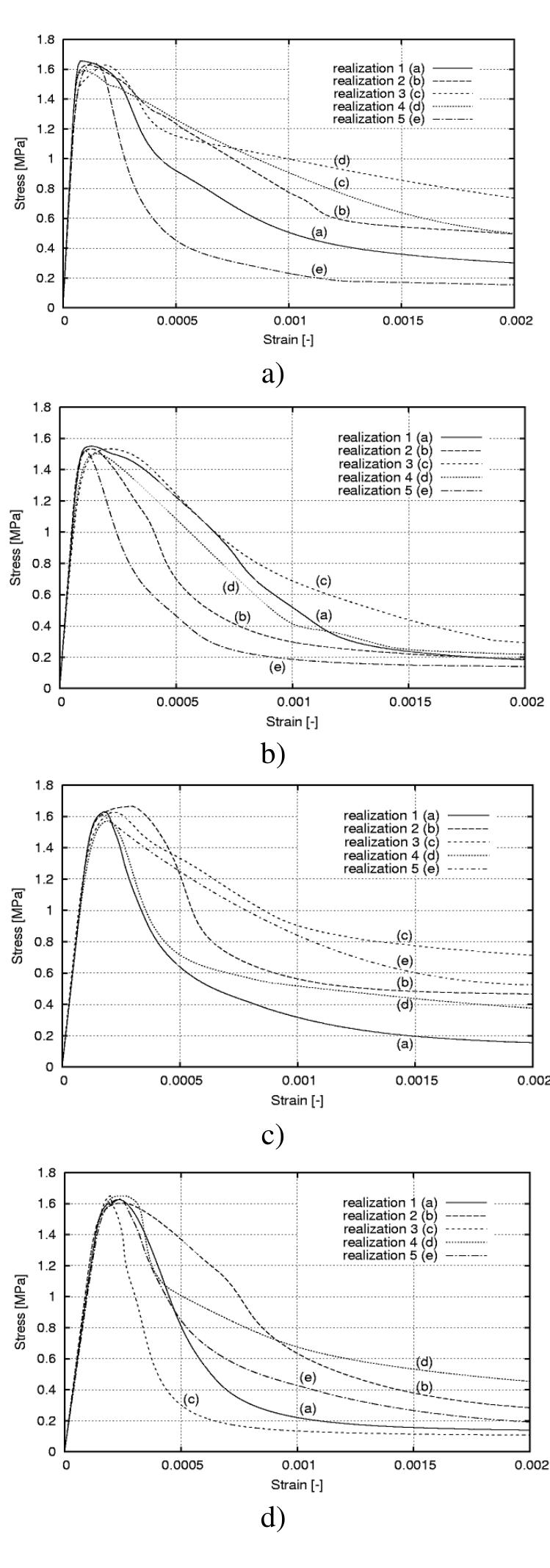


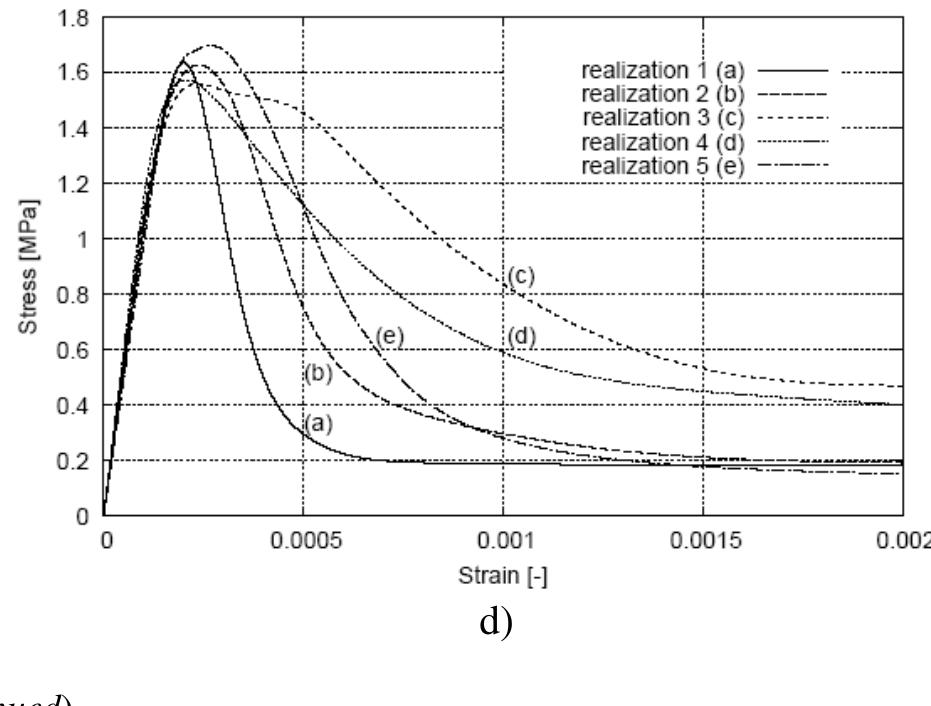












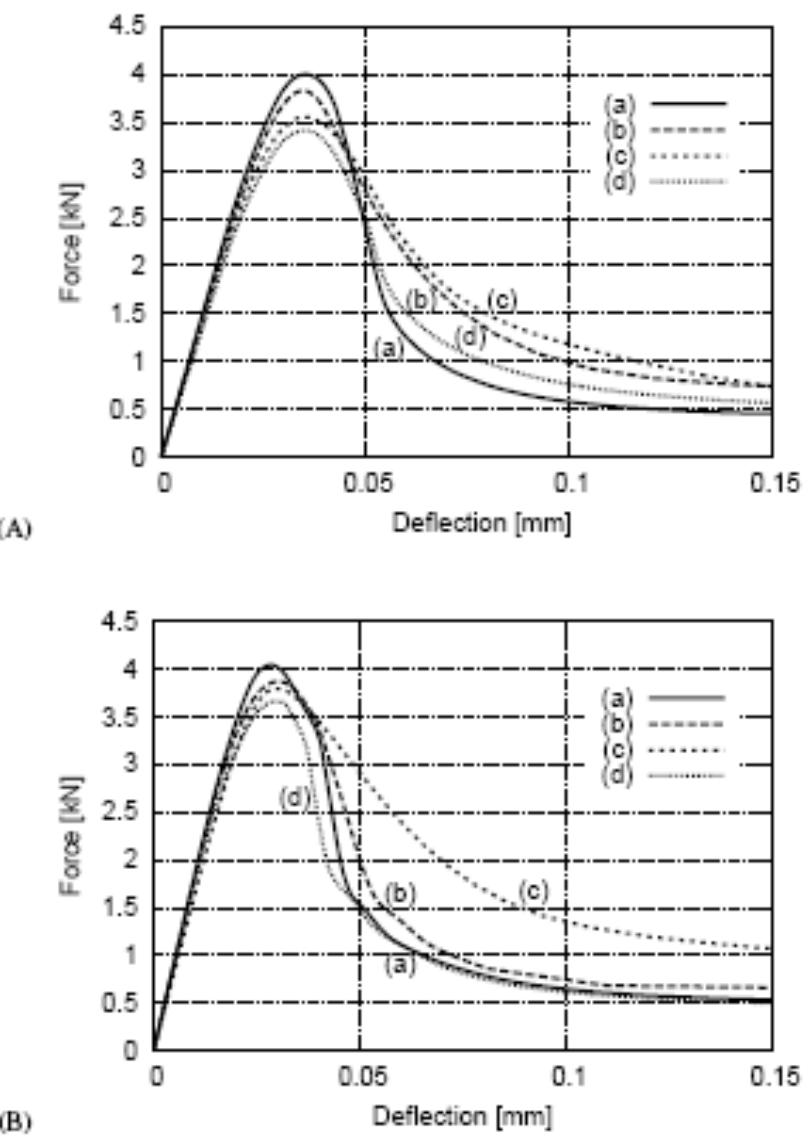
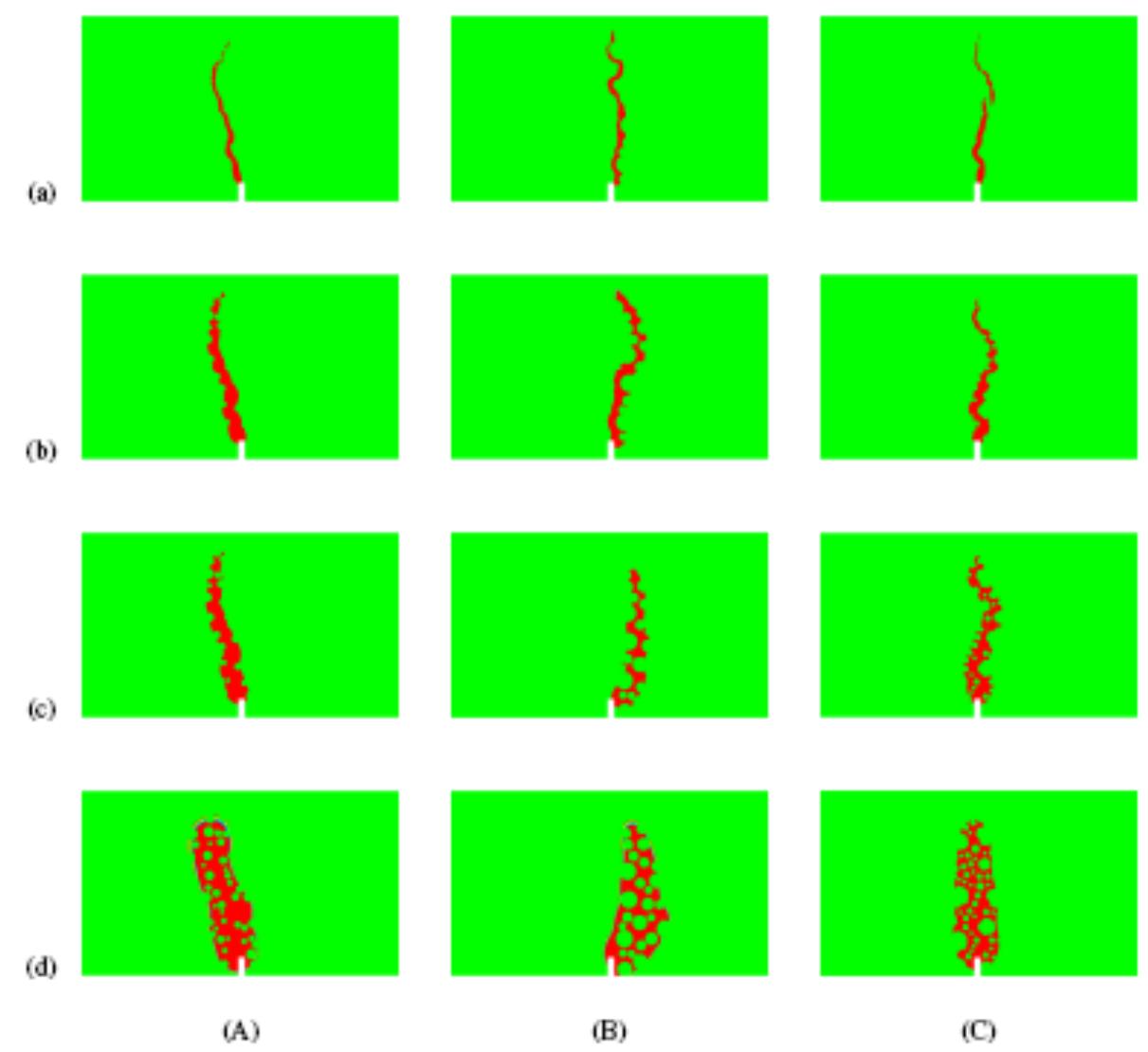
![Fig. 9.23 Formation of localized zone with mean width of w,=3.5-4.0 mm directly above notch in 3 different experiments (‘a’, ‘b’ and ‘c’) with small-size notched fine-grained concrete beam 80x320x40 mm? using DIC (vertical and horizontal axes denote coordinates in [mm] and colour scales strain intensity) (Skarzynski et al. 2011) digital images taken at a constant time increment from a professional digital camera (based on displacements, strains can be calculated) (White et al. 2003). The experimental set-up and results were described in detail by Skarzynski et al. (2011). The beams of the same size were also used by Le Bellégo et al. (2003). Figure 9.23 shows the formation of a localized zone on one side of the surface of a fine-grained small-size concrete beam above the notch from laboratory tests](https://figures.academia-assets.com/37013038/figure_344.jpg)













































Key takeaways
- The differences concern the height and shape of localized zones, • the FE-results are similar within two different continuum crack models, although a slightly better agreement with experiments was achieved with a damage model, • the beam strength increases mainly with increasing reinforcement ratio, characteristic length, tensile strength, fracture energy and decreasing beam size and shear span ratio.
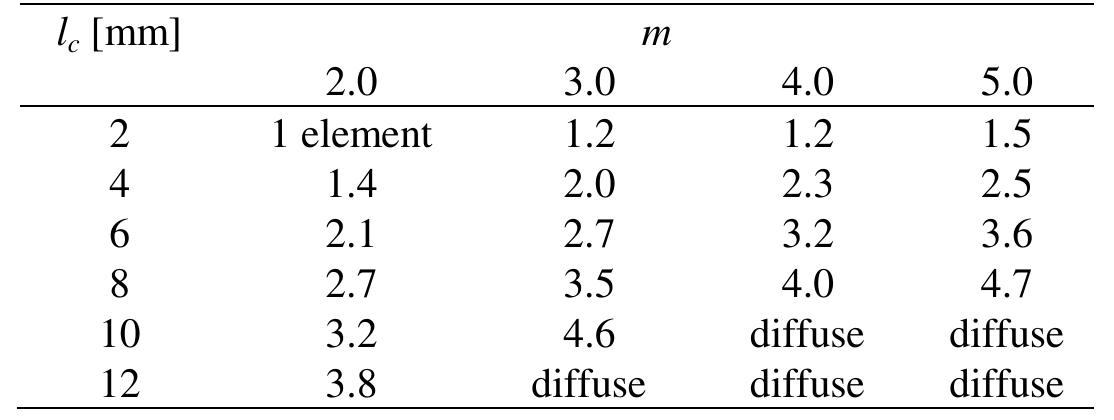
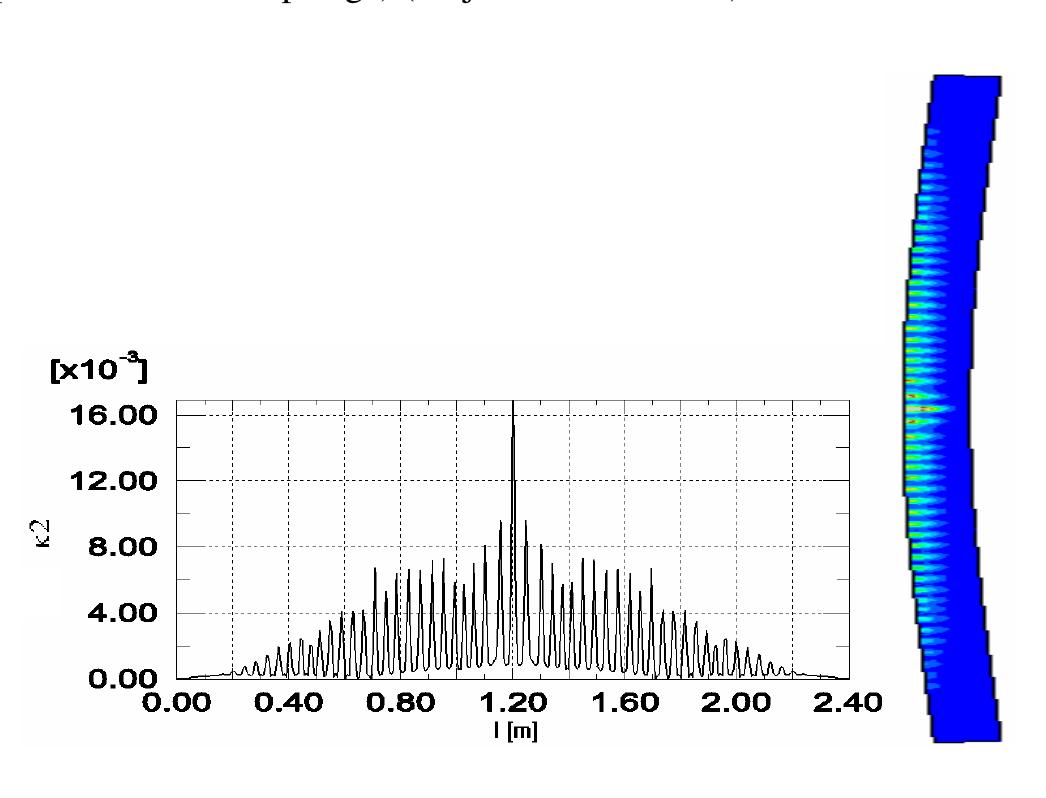
- The width is about (3-4)×l c , • the spacing of localized zones increases with increasing characteristic length l c , tensile softening modulus and decreasing fracture energy, reinforcement ratio and initial bond stiffness.
- Thus, the isotropic damage model needs improvements to describe localized shear zones in reinforced concrete elements under shear-tension failure, • the calculated spacing of localized tensile zones increased with increasing characteristic length, softening rate and beam height and decreasing fracture energy and bond stiffness.
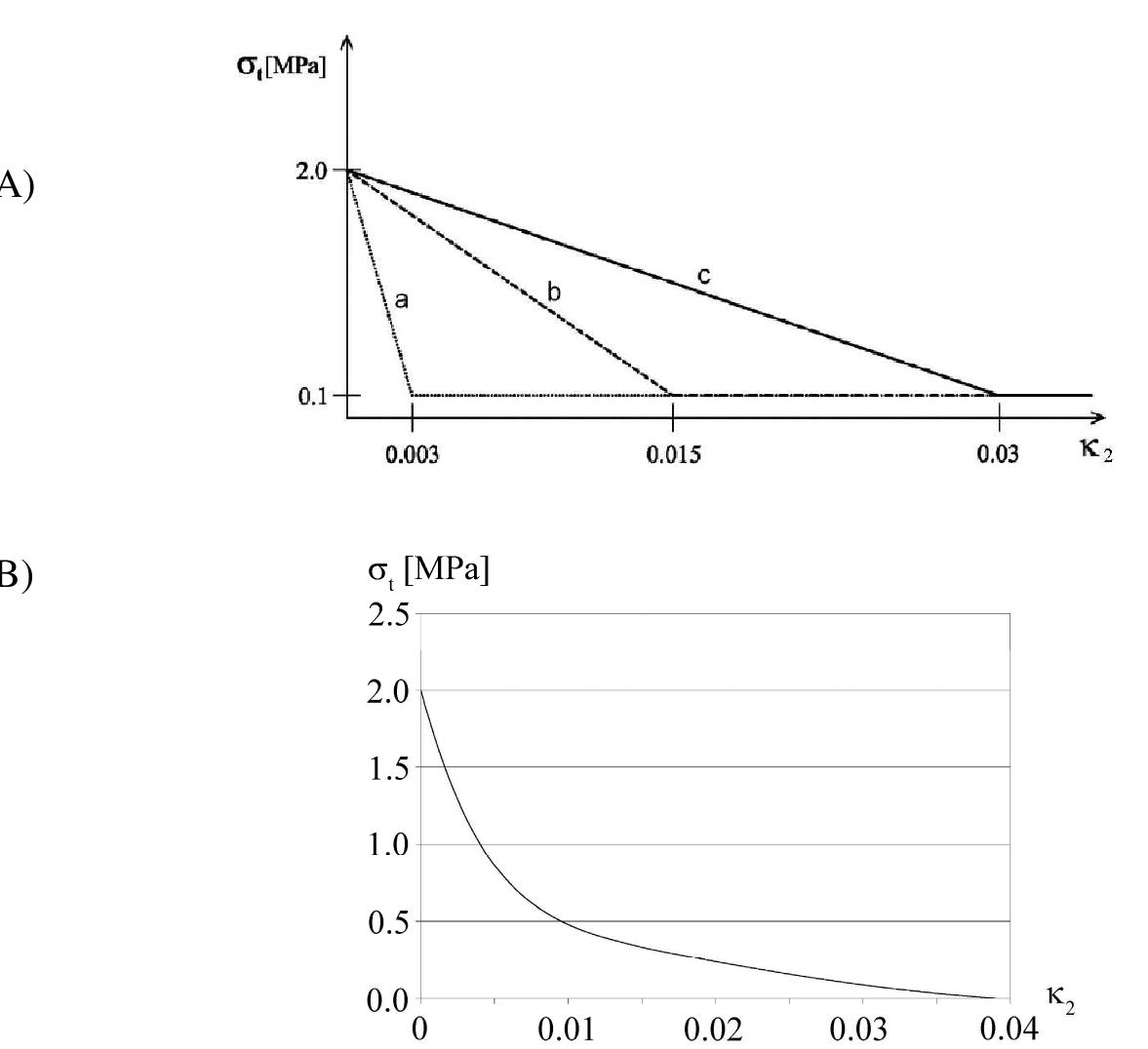
- To model the concrete softening under tension, the exponential curve by with the tensile strength of the concrete of f t =3.6 MPa was assumed (κ u =0.005 b 1 =3.0, b 2 =6.93) (Eq.
- For instance, in our other tests with large reinforced concrete beams 6.0 m long without shear reinforcement under bending, the width of a localized zone in usual concrete was about 15 mm indicating that l c =5 mm .
Related papers
International Journal for Numerical and Analytical Methods in Geomechanics, 2012
A new phenomenological macroscopic constitutive model for the numerical simulation of quasi-brittle fracture and ductile concrete behavior, under general triaxial stress conditions, is presented. The model is particularly addressed to simulate a wide range of confinement stress states, as also, to capture the strong influence of the mean stress value in the concrete failure mechanisms.
2015
The paper describes two-dimensional meso-scale results of fracture in notched concrete beams under bending. Concrete was modelled as a random heterogeneous 4-phase material composed of aggregate particles, cement matrix, interfacial transitional zones and air voids. Within continuum mechanics, the simulations were carried out with the finite element method based on a isotropic damage constitutive model enhanced by a characteristic length of micro-structure. In addition, the discrete element method was used. The concrete micro- structure in calculations was directly taken from real concrete specimens based on 3D x-ray micro-computed tomography images and 2D images by the scanning electron microscope. ovides information and instructions for preparing a Full Paper to be included in the Proceedings of COMPLAS XIII Conference.
Materials and Structures, 2008
A recently developed FE-based mesostructural model for the mechanical behavior of heterogeneous quasi-brittle materials is used systematically to analyze concrete specimens in 2D. The numerical model is based on the use of zero-thickness interface elements equipped with a normal-shear traction-separation constitutive law representing nonlinear fracture, which may be considered a mixedmode generalization of Hillerborg's ''Fictitious Crack Model.'' Specimens with 4 9 4 and 6 9 6 arrays of aggregates are discretized into finite elements. Interface elements are inserted along the main lines in the mesh, representing potential crack lines. The calculations presented in this paper consist of uniaxial tension loading, and the continuum elements themselves are assumed to behave as linear elastic. In this way, the influence of various aspects of the heterogeneous geometry and interface parameters on the overall specimen response has been investigated. These aspects are aggregate volume fraction, type of arrangement and geometry, interface layout, and values of the crack model parameters chosen for both the aggregate-aggregate and matrix-aggregate interfaces. The results show a good qualitative agreement with experimental observations and illustrate the capabilities of the model. In the companion second part of the paper, the model is used to represent other loading states such as uniaxial compression, Brazilian test, or biaxial loading.
Mechanics Research Communications, 2017
On the basis of the strong discontinuity analysis, a discrete model expressed in terms of traction vectordisplacement jump has been constructed from a continuous model expressed in terms of stress-strain law. In the first part of the paper, this approach has been extended to a class of anisotropic continuum damage constitutive models [1]. In this second part of the paper, the proposed class of discrete anisotropic damage constitutive models is particularized. More precisely, a micromechanical-based anisotropic damage constitutive model is derived. This model accounts in a natural manner for particular crack families orientation. The aims of this paper are (i) to illustrate the capabilities of the proposed discrete enhanced model in reproducing the induced anisotropy appearing in quasi-brittle materials when cracking and (ii) to assess the numerical robustness of the time integration scheme. For this purpose, two numerical examples at the material point level are exposed after a brief presentation of the time integration scheme. The correspondence between the continuous and the discrete model as well as the induced anisotropy features are emphasized.
Engineering Fracture Mechanics, 2010
A coupled plasticity-damage model for plain concrete is presented in this paper. Based on continuum damage mechanics (CDM), an isotropic and anisotropic damage model coupled with a plasticity model is proposed in order to effectively predict and simulate plain concrete fracture. Two different damage evolution laws for both tension and compression are formulated for a more accurate prediction of the plain concrete behavior. In order to derive the constitutive equations and for the easiness in the numerical implementation, in the CDM framework the strain equivalence hypothesis is adopted such that the strain in the effective (undamaged) configuration is equivalent to the strain in the nominal (damaged) configuration. The proposed constitutive model has been shown to satisfy the thermodynamics requirements. Detailed numerical algorithms are developed for the finite element implementation of the proposed coupled plasticity-damage model. The numerical algorithm is coded using the user subroutine UMAT and then implemented in the commercial finite element analysis program Abaqus. Special emphasis is placed on identifying the plasticity and damage model material parameters from loading–unloading uniaxial test results. The overall performance of the proposed model is verified by comparing the model predictions to various experimental data, such as monotonic uniaxial tension and compression tests, monotonic biaxial compression test, loading–unloading uniaxial tensile and compressive tests, and mixed-mode fracture tests.
Continuum Mechanics and Thermodynamics, 2010
The aim of this study is to propose a model describing the evolution of the mechanical properties of micro-cracked bodies under slow mechanical loading. To do so, we consider each material element of the body as a domain of finite size comprising one single crack. The size and orientation of the latter are treated as Lagrangian coordinates that are complementary to those usually describing the translations of the material elements. As such, their evolution is driven by some balance equations that are provided by the theory of continua with microstructure and by fit constitutive equations. To deal with the latter, we then call upon fracture mechanics. The model is applied to concrete within some simplifying assumptions and the case of a bar tensioned by a hard device is studied. Crack propagation and stiffness loss are determined when the loading increases, they are compared to experimental results.
2003
Modelling concrete continuum models, namely a single parameter isotropic damage model (SDM) and a rotating crack model (RCM), are analysed, developed and implemented into an existing modular computer program (FEMAS, Finite Element Modulus of Arbitrary Structures, Ruhr-Universität Bochum, Germany). These models are of interest not only for concrete but also for other-so-called quasi-brittle-materials (such as masonry, rocks and some kind of soils), which are frequently used by civil engineers. 3. PHYSICAL PARAMETERS CHARACTERIZING TENSIONAL CRACKING Cracking and consequent loss of mechanical properties occur due to the proliferation and the coalescence of micro-defects and micro-voids, which exist in concrete even before the application of any external action.
2010
A meso-scale analysis is performed to determine the fracture process zone of concrete subjected to uniaxial tension. The meso-structure of concrete is idealised as stiff aggregates embedded in a soft matrix and separated by weak interfaces. The mechanical response of the matrix, the inclusions and the interface between the matrix and the inclusions is modelled by a discrete lattice approach. The inelastic response of the lattice elements is described by a damage approach, which corresponds to a continuous reduction of the stiffness of the springs. The fracture process in uniaxial tension is approximated by an analysis of a two-dimensional cell with periodic boundary conditions. The spatial distribution of dissipated energy density at the meso-scale of concrete is determined. The size and shape of the deterministic FPZ is obtained as the average of random meso-scale analyses. Additionally, periodicity of the discretisation is prescribed to avoid influences of the boundaries of the periodic cell on fracture patterns. The results of these analyses are then used to calibrate an integral-type nonlocal model.
The effects of the descending branch of the tensile stress-strain curve, fracture energy, grid refinement, and load-step size on the response of finite element models of notched concrete beams are studied. The width of the process zone and constraint of crack angles are investigated. Nonlinearity is limited to cracking of the concrete. A limiting tensile stress criteria n governs crack initiation. Concrete is represented as linear elastic prior to cracking. Cracks are modeled using a smeared representa ion. The post-crackir.g behavior is controlled by the shape of the descending branch, fracture energy, crack angle, and element size. Unloading occurs at a slope equal to the initial modulus of the material. Load-deflection curves and cracking patterns are used to evaluate the beam's response. Com pari sons of the process zone size are made. All analyses are performed on a 200 X 200 X GOO mm concrete beam, with an initial notch length of 80 mm. The fracture energy, tensile strength, and shape of the descending branch interact to determine the stiffness and general behavior of the specimen. The width of the process zone has a negligible influence on the beam's response. The importance of proper crack orientation is demonstrated. The model is demonstrated to be objective with respect to grid refinement and load-step size. 17. Document Analysis a. Descriptors (fracturing), concrete, crack localization, cracking finite elements, fracture mechanics, fracture process zone, load-deflection, s tructura 1 engineering, tension softening, unloading b. Identifiers/Open-Ended Terms c. COSATI Field/Group 18. Availability Statement 19. Security Class (This Report)

Loading Preview
Sorry, preview is currently unavailable. You can download the paper by clicking the button above.
Related papers
Engineering Fracture Mechanics, 2008
International Journal of Solids and Structures, 2011
Computers & Structures, 2011
Computers & concrete, 2010
Computers and Concrete, 2008
Mechanics of Cohesive‐frictional Materials, 1996
International Journal for Numerical and Analytical Methods in Geomechanics, 2003
International Journal of Solids and Structures, 2012
Fatigue & Fracture of Engineering Materials & Structures, 2006