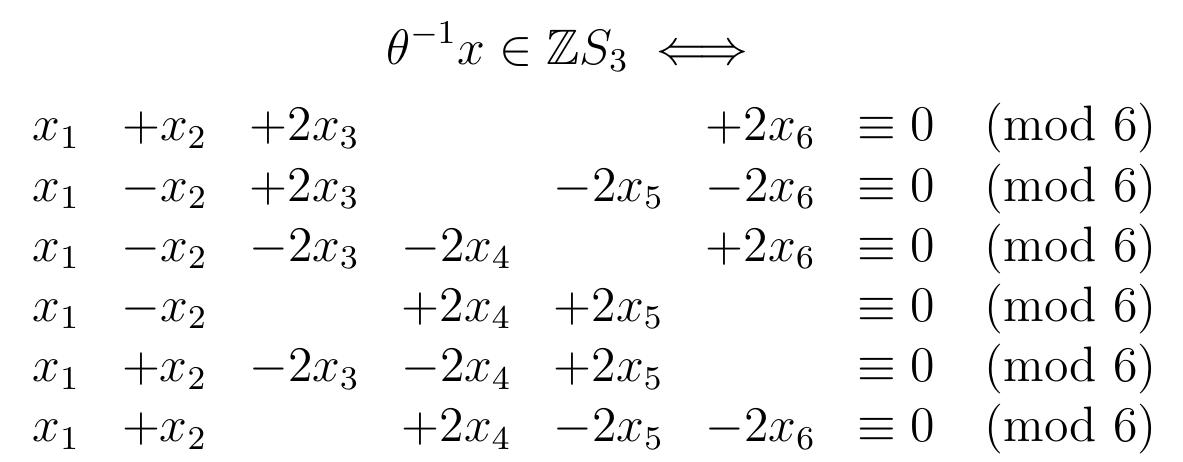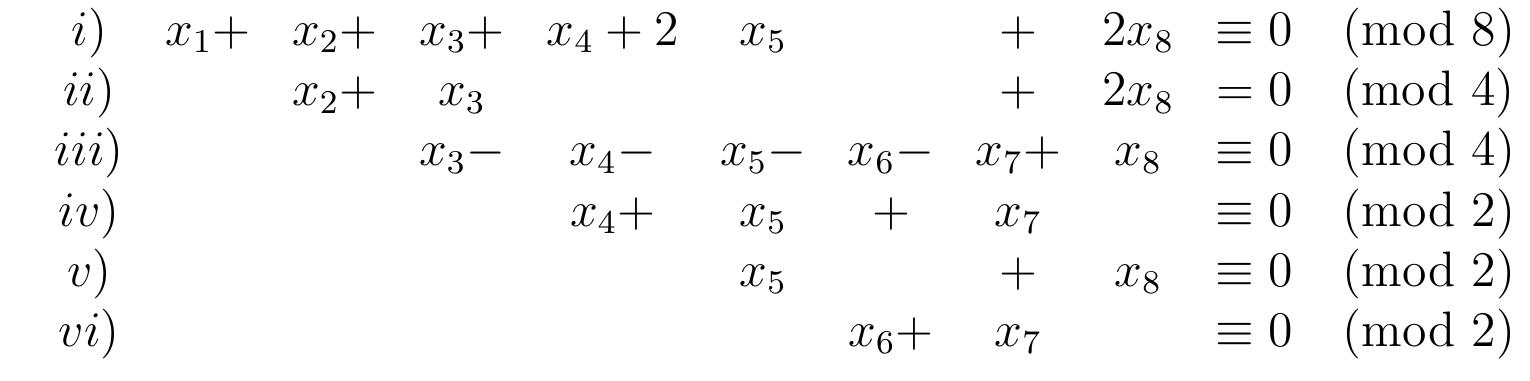High Energy Physics

El análisis de los incentivos regionales sobre las decisiones de localización empresarial ha sido objeto de gran interés por parte de la economía regional. Sin embargo, son escasos los estudios que han contrastado en términos de probabilidad las predicciones de los modelos teóricos con datos georreferenciados de  empresas. En este trabajo se analiza el impacto de las ayudas regionales en la estructura sectorial  de las empresas del Corredor del Henares comparando las predicciones obtenidas a partir de múltiples simulaciones con los esquemas de localización observados en la base de datos SABI. La metodología aplicada en las simulaciones es la denominada basada en agentes. En lugar de simular el comportamiento general del fenómeno objeto de estudio, se define el comportamiento individual de los agentes implicados y se establecen las reglas generales de interacción entre los mismos para a partir de ellos obtener sus comportamientos emergentes. Los resultados obtenidos indican que los incentivos regionales además de favorecer el desplazamiento de las empresas hacia las zonas con ayudas generan nuevos entornos que favorecen el surgimiento en las zonas sin ayudas de nuevas empresas de características –y sectores- diferentes a las que de otro modo hubieran surgido.

A nonrelativistic particle on a circle and subject to a cos^{-2}(k phi) potential is related to the two-dimensional (dihedral) Coxeter system I_2(k), for k in N. For such `dihedral systems' we construct the action-angle variables and establish a local equivalence with a free particle on the circle. We perform the quantization of these systems in the action-angle variables and discuss the supersymmetric extension of this procedure. By allowing radial motion one obtains related two-dimensional systems, including A_2, BC_2 and G_2 three-particle rational Calogero models on R, which we also analyze.

We propose the integrable (pseudo)spherical generalization of the fourdimensional anisotropic oscillator with additional nonlinear potential. Performing its Kustaanheimo–Stiefel transformation we then obtain the pseudospherical generalization of the MICZ-Kepler system with linear and cos θ potential terms. We also present the generalization of the parabolic coordinates, in which this system admits the separation of variables. Finally,
we get the spherical analog of the presented MICZ-Kepler-like system.

It is shown that for a central potential that is an injective function of the radial coordinate, a second central potential can be found that leads to trajectories in the configuration space and the momentum space coinciding, respectively, with the trajectories in the momentum space and the configuration space produced by the original potential.

Although the MiniBooNE experiment has severely restricted the possible existence of light sterile neutrinos, a few anomalies persist in oscillation data, and the possibility of extra light species contributing as a subdominant hot (or warm) component is still interesting. In many models, this species would be in thermal equilibrium in the early universe and share the same temperature as active neutrinos, but this is not necessarily the case. In this work, we fit up-to-date cosmological data with an extended ΛCDM model, including light relics with a mass typically in the range 0.1–10 eV. We provide, first, some nearly model-independent constraints on their current density and velocity dispersion, and second, some constraints on their mass, assuming that they consist either in early decoupled thermal relics, or in nonresonantly produced sterile neutrinos. Our results can be used for constraining most particle-physics-motivated models with three active neutrinos and one extra light species. For instance, we find that at the 3σ confidence level, a sterile neutrino with mass ms=2  eV can be accommodated with the data provided that it is thermally distributed with Ts/Tνid≲0.8 or nonresonantly produced with ΔNeff≲0.5. The bounds become dramatically tighter when the mass increases. For ms≲0.9  eV and at the same confidence level, the data is still compatible with a standard thermalized neutrino.

We point out that the exchange of a Goldstone pseudo-scalar can provide an enhancement in the dark matter annihilation rate capable of explaining the excess flux seen in high energy cosmic ray data. The mechanism of enhancement involves the coupling of s and d waves through the tensor force that is very strong and, in fact, singular at short distances. The results indicate that large enhancements require some amount of fine tuning. We also discuss the enhancement due to other singular attractive potentials, such as WIMP models with a permanent electric dipole.

The subatomic particle mass spectrum in the 100 MeV to 7,000 MeV range is retrodicted to a first approximation using the Kerr solution of General Relativity.  The particle masses appear to form a restricted set of quantized values of the Kerr solution: n1/2 M, where values of n are a set of discrete integers and M is the revised Planck mass.  The accuracy of the 27 retrodicted masses averages 98.4%.  Discrete Scale Relativity is required to evaluate M, which differs from the conventional Planck mass by a factor of roughly 1019.

In the setting of C*-categories, we provide a definition of "spectrum" of a commutative full C*-category as a one-dimensional unital saturated Fell bundle over a suitable groupoid (equivalence relation) and prove a categorical Gelfand duality theorem generalizing the usual Gelfand duality between the categories of commutative unital C*-algebras and compact Hausdorff spaces.
Although many of the individual ingredients that appear along the way are well-known, the somehow unconventional way we "glue" them together seems to shed some new light on the subject.

A Banach involutive algebra (A, ∗) is called a Krein C*-algebra if there is a fundamental symmetry of (A, ∗), i.e., α ∈ Aut (A, ∗) such that α^2 = Id_A and ||α(x∗ )x|| = ||x||^2 for all x ∈ A. Using α, we can decompose A = A_+ ⊕ A_−, where A+ = {x ∈ A | α(x) = x} and A− = {x ∈ A | α(x) = −x}. The even part A_+ is a C*-algebra and the odd part A_− is a Hilbert C*-bimodule over the even part A+ . The ultimate goal is to develop a spectral theory for commutative Krein C*-algebras when the odd part is an imprimitivity bimodule over the commutative even part.

After an introduction to some basic issues in non-commutative geometry (Gel'fand duality, spectral triples), we present a "panoramic view" of the status of our current research program on the use of categorical methods in the setting of A.Connes' non-commutative geometry: morphisms/categories of spectral triples, categorification of Gel'fand duality. We conclude with a summary of the expected applications of "categorical non-commutative geometry" to structural questions in relativistic quantum physics: (hyper)covariance, quantum space-time, (algebraic) quantum gravity.

The cross sections for a variety of diffractive processes in proton-nucleus scattering, associated with large gaps in rapidity, are calculated within an improved Glauber-Gribov theory, where the inelastic shadowing corrections are summed to all orders by employing the dipole representation. The effects of nucleon correlations, leading to a modification of the nuclear thickness function, are also taken into account. Numerical calculations are performed for the energies of the HERA-B experiment, and the RHIC and LHC colliders, and for several nuclei. It is found that whereas the Gribov corrections generally make nuclear matter more transparent, nucleon correlations act in the opposite direction and have important effects in various diffractive processes.

Non scaling Fixed-Field Alternating Gradient (FFAG accelerators have an unprecedented potential for muon acceleration, as well as for medical purposes based on carbon
and proton hadron therapy. They also represent a possible active element for an Accelerator Driven Subcritical Reactor (ADSR). Starting from first principle the Hamiltonian formalism for the description of the dynamics of particles in non-scaling FFAG machines has been developed. The stationary reference (closed) orbit has been found within the Hamiltonian framework. The dependence of the path length on the energy
deviation has been described in terms of higher order dispersion functions. The latter have been used subsequently to specify the longitudinal part of the Hamiltonian. It has been shown that higher order phase slip coecients should be taken into account to adequately describe the acceleration in non-scaling FFAG accelerators. A complete theory of the fast (serpentine) acceleration in non-scaling FFAGs has been developed. An example of the theory is presented for the parameters of the Electron Machine with Many Applications (EMMA), a prototype electron non-scaling FFAG to be hosted at
Daresbury Laboratory.

We investigate finite 3-nets embedded in a projective plane over a (finite or infinite) field of any characteristic p. Such an embedding is regular when each of the three classes of the 3-net comprises concurrent lines, and irregular otherwise. It is completely irregular when no class of the 3-net consists of concurrent lines.
We are interested in embeddings of 3-nets  which are irregular but the lines of one class are concurrent. For an irregular embedding of a 3-net of order n> 4 we prove that,  if all lines from  two classes are tangent to the same irreducible conic,  then all lines from the third class are concurrent. We also prove the converse provided that the order n of the 3-net is smaller than p. In the complex plane, apart from a sporadic example of order n=5 due to Stipins, each known irregularly embedded 3-net has the property that all its lines are tangent to a plane cubic curve. Actually, the procedure of constructing irregular 3-nets with this property works over any field. In positive characteristic, we present some more examples for n>5 and  give a complete classification for n=4.

We provide combinatorial as well as probabilistic interpretations for the q-analogue of the Pochhammer k-symbol introduced by Diaz and Teruel. We introduce q-analogues of the Mellin transform in order to study the q-analogue of the k-gamma distribution.

We consider the nuclear scattering cross section for the eXciting Dark Matter (XDM) model. In XDM, the Weakly Interacting Massive Particles (WIMPs) couple to the Standard Model only via an intermediate light scalar which mixes with the Higgs: this leads to a suppression in the nuclear scattering cross section relative to models in which the WIMPs couple to the Higgs directly. We estimate this suppression factor to be of order 10^(-5). The elastic nuclear scattering cross section for XDM can also be computed directly: we perform this computation for XDM coupled to the Higgs sector of the Standard Model and find a spin-independent cross section in the order of 4 x 10^(-13) pb in the decoupling limit, which is not within the range of any near-term direct detection experiments. However, if the XDM dark sector is instead coupled to a two-Higgs-doublet model, the spin-independent nuclear scattering cross section can be enhanced by up to four orders of magnitude for large tan(beta), which should be observable in the upcoming SuperCDMS and ton-scale xenon experiments.

This thesis deals with the problem of describing the unit group of specific group rings over the integers. Some results are given in an expository manner as the proofs of the results are normally very dependent on the particular group. The ones presented by this method later on are S3,D4,D6 and A4.
Next, we present the method for groups of order p3, where p is an odd prime.
These come from a paper by Ritter and Sehgal. I consider both non-abelian groups of order p3 and descriptions of the unit groups of both of their respective group rings are presented.I present the method as applied to the groups of order 27.
The last theoretical results are on determining the unit group of the group ring over a group of order pq where p ≡ 1( mod q). These results come from a paper by Luthar [3]. No practical examples are done of this method.
The next part deals with presenting actual groups and determining the unit structure of their integral group ring. The first two, S3 and D4 are from previous authors. The first was done by Hughes and Pearson [2], the second by C. Polcino-
Milies [4]. I also present, D6, which is new result of the thesis.

The scale invariance of the source-free Einstein field equations suggests that one might be able to model hadrons as “strong gravity” black holes, if one uses an appropriate rescaling of units or a revised gravitational coupling factor.  The inner consistency of this hypothesis is tested by retrodicting a close approximation to the mass of the proton from an equation that relates the angular momentum and mass of a Kerr black hole.  More accurate mass and radius values for the proton are then retrodicted using the geometrodynamic form of the full Kerr-Newman solution of the Einstein-Maxwell equations.  The radius of an alpha particle is calculated as an additional retrodictive test.  In a third retrodictive test of the “strong gravity” hypothesis, the subatomic particle mass spectrum in the 100 MeV to 7,000 MeV range is retrodicted to a first approximation using the Kerr solution of General Relativity.  The particle masses appear to form a restricted set of quantized values of the Kerr solution: (sqrt n)(M), where values of n are a set of discrete integers and M is the revised Planck mass.  The accuracy of the 27 retrodicted masses averages 98.4%.  Finally, the new atomic scale gravitational coupling constant suggests a radical revision of the assumptions governing the Planck scale, and leads to a natural explanation for the fine structure constant.

We consider the Klein-Gordon equation in generalized higher-dimensional Kerr-NUT-(A)dS spacetime without imposing any restrictions on the functional parameters characterizing the metric. We establish commutativity of the second-order operators constructed from the Killing tensors found in [J. High Energy Phys. 02 (2007) 004] and show that these operators, along with the first-order operators originating from the Killing vectors, form a complete set of commuting symmetry operators (i.e., integrals of motion) for the Klein-Gordon equation. Moreover, we demonstrate that the separated solutions of the Klein-Gordon equation obtained in [J. High Energy Phys. 02 (2007) 005] are joint eigenfunctions for all of these operators. We also present an explicit form of the zero mode for the Klein-Gordon equation with zero mass. In the semiclassical approximation we find that the separated solutions of the Hamilton-Jacobi equation for geodesic motion are also solutions for a set of Hamilton-Jacobi-type equations which correspond to the quadratic conserved quantities arising from the above Killing tensors.

The theoretical vacuum energy density estimated on the basis of the Standard Model of particle physics and very general quantum assumptions is 59 to 123 orders of magnitude larger than the measured vacuum energy density for the observable universe which is determined on the basis of the Standard Model of cosmology and empirical data.  This enormous disparity between the expectations of two of our most widely accepted theoretical frameworks demands a credible and self-consistent explanation, and yet even after decades of sporadic effort a generally accepted resolution of this crisis has not surfaced.  Very recently, however, a discrete self-similar cosmological paradigm based on the fundamental principle of discrete scale invariance has been found to offer a rationale for reducing the vacuum energy density disparity by at least 115 orders of magnitude, and possibly this new paradigm offers a means of eliminating the vacuum energy density crisis entirely.

This book addresses the question: why do more girls than boys choose to continue studying mathematics in England? It discusses the issue using interviews with young people aged 16-19 who did choose to continue with mathematics. It uses a feminist post-structural framework.

The book is published by Open University Press.

We survey recent work on non-linear recurrence equations that arise in computer science or combinatorics. We consider the examples of the height of digital trees, the QUICKSORT algorithm, height of binary search trees, and enumeration problems concerning random binary trees characterized by nodes and path lengths. In each case a singular perturbation analysis of the recurrence yields insights into the asymptotic behavior, such as limiting distributions and tail probabilities.

Since a Lie group, G, is a smooth manifold, we can endow G with a Riemannian metric. Among all the Riemannian metrics on a Lie groups, those for which the left translations (or the right translations) are isometries are of particular interest because they take the group structure of G into account. As a consequence, it is possible to find explicit formulae for the Levi-Civita connection and the various curvatures, especially in the case of metrics which are both left and right-invariant. This chapter makes extensive use of results from a beautiful paper of Milnor .

Given a manifold, M , in general, for any two points, p, q ∈ M , there is no "natural" isomorphism between the tangent spaces T p M and T q M . More generally, given any vector bundle, ξ = (E, π, B, V ), for any two points, p, q ∈ B, there is no "natural" isomorphism between the fibres, E p = π −1 (p) and E q = π −1 (q). Given a curve, c : [0, 1] → M , on M (resp. a curve, c : [0, 1] → E, on B), as c(t) moves on M (resp. on B), how does the tangent space, T c(t) M (resp. the fibre E c(t) = π −1 (c(t))) change as c(t) moves?

In this paper we propose a 3D image reconstruction algorithm for a 3D Compton camera being developed at the University of Michigan. We present a mathematical model of the transition matrix of the camera which exploits symmetries by using an adapted spatial sampling pattern in the object domain. For each projection angle, the sampling pattern is uniform over a set of equispaced nested hemispheres. By using this sampling pattern the system matrix is reduced to a product of a (approximately) block circulant matrix and a sparse interpolation matrix. This representation reduces the very high storage and computation requirement inherent to 3D reconstruction using transition matrix inversion methods. We geometrically optimize our hemispherical sampling and propose a 3D volumetric interpolation. Finally, we present a 3D image reconstruction method which uses the Gauss-Seidel algorithm to minimize a penalized least square objective.

In this paper we propose a 3D image reconstruction algorithm for a 3D Compton camera being developed at the University of Michigan. We present a mathematical model of the transition matrix of the camera which exploits symmetries by using an adapted spatial sampling pattern in the object domain. For each projection angle, the sampling pattern is uniform over a set of equispaced nested hemispheres. By using this sampling pattern the system matrix is reduced to a product of a (approximately) block circulant matrix and a sparse interpolation matrix. This representation reduces the very high storage and computation requirement inherent to 3D reconstruction using transition matrix inversion methods. We geometrically optimize our hemispherical sampling and propose a 3D volumetric interpolation. Finally, we present a 3D image reconstruction method which uses the Gauss-Seidel algorithm to minimize a penalized least square objective.

An apology is an explanation or defense of actions which may otherwise be misunderstood. There are several sources of misunderstanding concerning the proof of the Riemann hypothesis. An obstacle lies in the narrow perception of the Riemann hypothesis as a mechanism for counting prime numbers. The Riemann hypothesis is significant because of its significance in mathematical analysis. The proof cannot be read as an isolated argument because of its roots in the history of mathematics. Another obstacle lies in the unexpected source of the proof of the Riemann hypothesis. The proof is made possible by events which seem at first sight to have no relevance to mathematics. Exceptional people and exceptional circumstances prepared the proof of the Riemann hypothesis.

We discuss some basic issues that arise when one attempts to model quantum mechanical systems on a computer, and we describe the mathematical structure of the resulting discretized cannonical commutation relations. The C *algebras associated with the discretized CCRs are the non-commutative spheres of Bratteli, Elliott, Evans and Kishimoto.

In probability theory all nonatomic probability measures look the same. That is because any two nonatomic separable measure algebras are isomorphic. Quantum probability theory is different: two normal states of B(H) are conjugate only when the eigenvalue lists of their density operators are the same. Suppose now that one is given an increasing sequence M 1 ⊆ M 2 ⊆ . . . of type I subfactors of B(H) whose union is weak * -dense in B(H). Common sense suggests that if one restricts a normal state ρ of B(H) to M n and considers its eigenvalue list Λ n for large n, then Λ n should be close to the eigenvalue list of ρ when n is large.

We initiate a study of Hilbert modules over the polynomial algebra A=C [z_1,...,z_d] that are obtained by completing A with respect to an inner product having certain natural properties. A standard Hilbert module is a finite multiplicity version of one of these. Standard Hilbert modules occupy a position analogous to that of free modules of finite rank in commutative algebra, and their quotients by submodules give rise to universal solutions of nonlinear relations.

If ψ is a bijection from C n onto a complex manifold M, which conjugates every holomorphic map in C n to an endomorphism in M, then we prove that ψ is necessarily biholomorphic or antibiholomorphic. This extends a result of A. Hinkkanen to higher dimensions. As a corollary, we prove that if there is an epimorphism from the semigroup of all holomorphic endomorphisms of C n to the semigroup of holomorphic endomorphisms in M, or an epimorphism in the opposite direction for a doubly-transitive M, then it is given by conjugation by some biholomorphic or antibiholomorphic map. We show also that there are two unbounded domains in C n with isomorphic endomorphism semigroups but which are neither biholomorphically nor antibiholomorphically equivalent.

This is one in a series of papers devoted to the foundations of Symplectic Field Theory sketched in [EGH]. We prove compactness results for moduli spaces of holomorphic curves arising in Symplectic Field Theory. The theorems generalize Gromov's compactness theorem in [Gr] as well as compactness theorems in Floer homology theory, [F1, F2], and in contact geometry, .